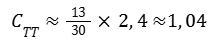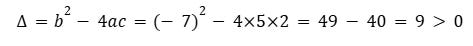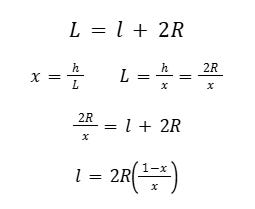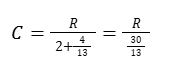Exclusive / Eng. G. Pierrez : The Hidden Geometry of the Nimitz' UAP Case
Engineer Guillaume Pierrez has found an intriguing ratio in the proportions of the ‘TicTac’ UFO.
A shape that disregards aerodynamics
During a Formula 1 race, would you be willing to bet on a participant showing up with square wheels? Probably not...
However, this is almost the kind of bet that the designers of the TIC TAC (if there is a design) could have taken.
As part of a supersonic aircraft design project, any aeronautical engineer would start with an arrowhead shape. This is in fact, what fluid mechanics recommend in order to promote air flow and minimize heating of the fuselage. It is therefore completely implausible to opt for the shape of a TIC TAC for a mobile with this capacity.
Although we don't know its flight technique, we already know one essential thing : shape seems to prevail over aerodynamics.
Is the phenomenon the result of a design?
Before continuing, it is appropriate to confirm or refute the artificiality of the phenomenon. Some will rightly argue that the behavior described by witnesses, the kinetics, and many other aspects leave no doubt about the artificial nature of the phenomenon. It is true that all of these elements constitute a very strong set of presumptions.
However, I believe that a more technical and objective approach is possible. Let me explain using a can of soda:
Consider your aluminum soda can. Think for a moment about those who designed it and the very first question they had to ask themselves :
“What dimensions provide optimal volume for minimal aluminum cost? »
If we consider a can is roughly comparable to a cylinder, we can describe its volume and its surface area based on its radius R and its height h. Then establish a relationship between Volume, cost and surface area. Without going into details, mathematics allows us to find the ideal solution.
In doing so, the resulting can literally bears the “mathematical trace” of its artificiality in its dimensions :
Now imagine an archaeologist from the future who finds the remains of your can. He will be able to measure the dimensions and will carry out the reverse reasoning to finally see with certainty the optimization effort. Because there is a very large number of possibilities but only one is optimized! Logically, he will conclude that this object was designed and produced by clever people.
Thus, if we consider that the object is artificial and cleverly designed, it is perhaps possible to find a "trace of optimization" in its geometry and its dimensions just as our archaeologist was able to find a trace of optimization in the shape of our can... Conversely, if we don't find anything conclusive, the mystery will remain unsolved...
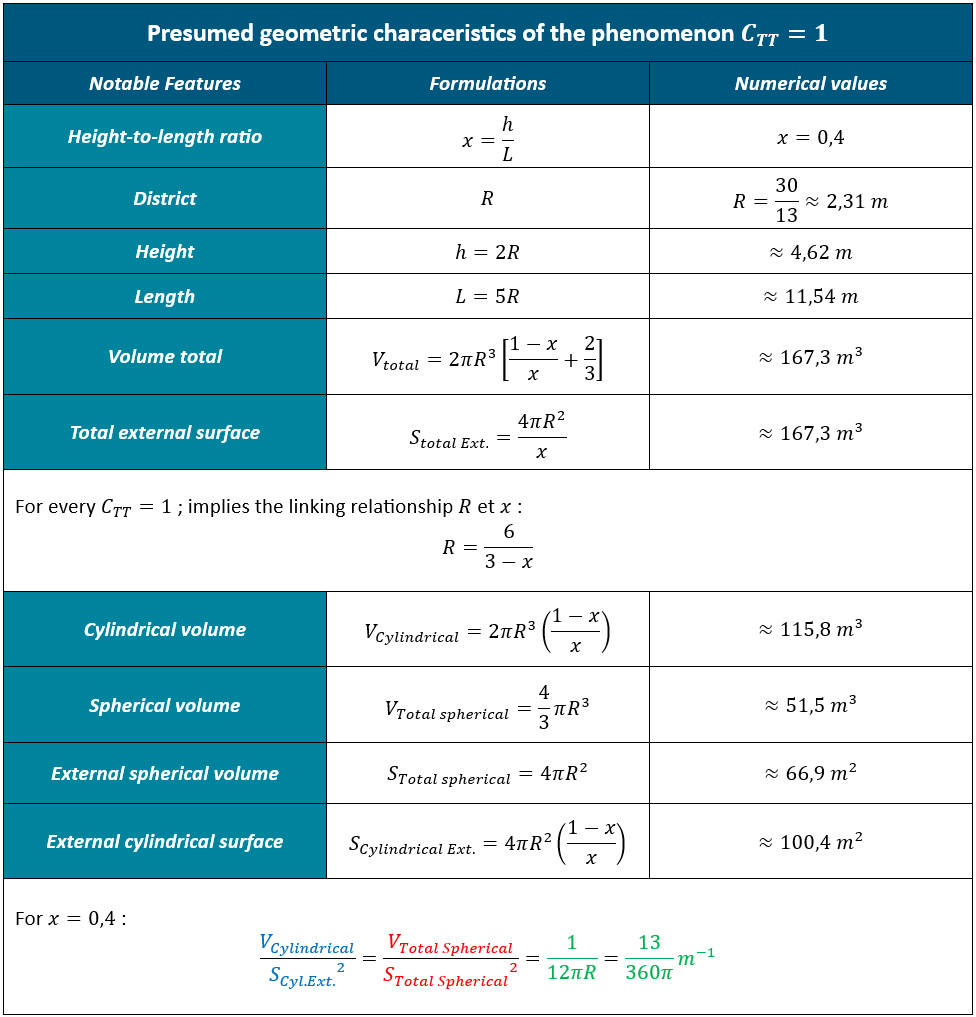
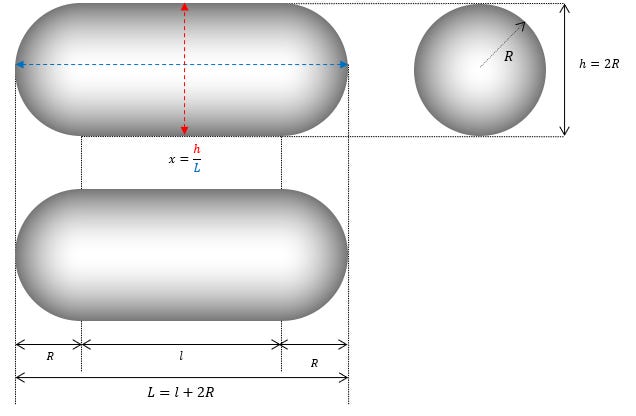
To begin, note that the form of a TIC TAC requires only two parameters (R and x) to define all possible solutions :
At this stage we can see that the geometry of the phenomenon includes two types of distinct surfaces :
This observation may seem trivial but it will prove essential later.
A cylindrical surface (side of the cylinder appearing in blue)
Two spherical surfaces (half-spheres at the ends in red)
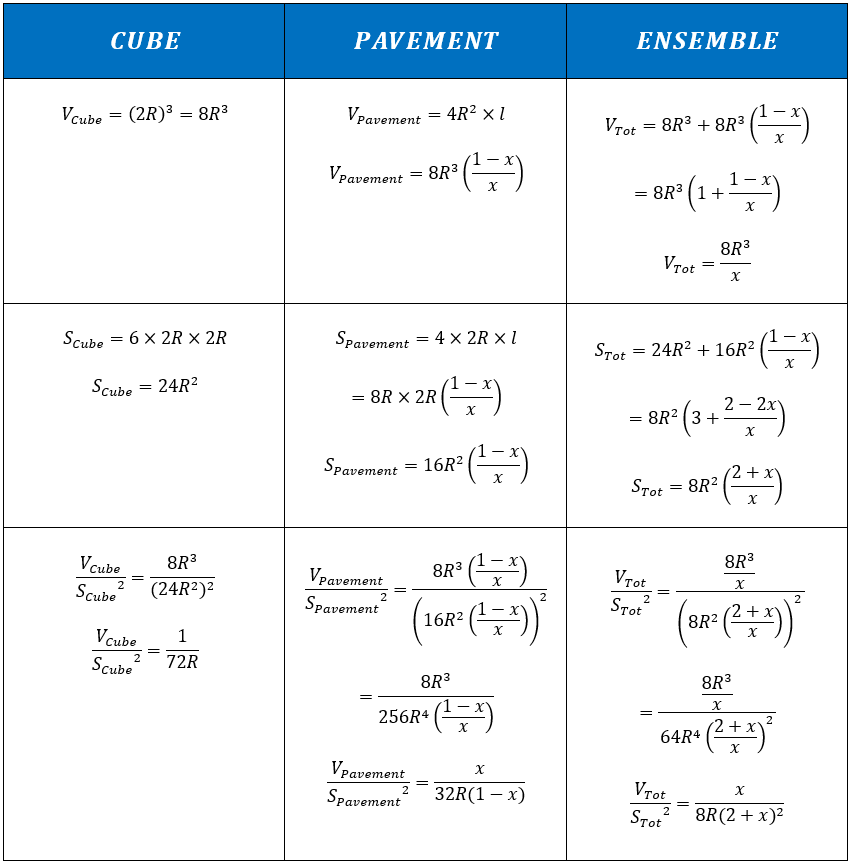
Now, let us mathematically describe the volumes and surfaces of each of these parts and compare them with each other using a matrix (details of the calculations available in annex 2) :
Nothing in particular emerges from this development. In fact, when R And x are indeterminate, no conclusive relationship seems to clearly emerge.
Let's now try the same approach by introducing one of the two values R or x. It is not possible to give an estimate of R that is sufficiently precise, on the other hand, based on the visible images of the FLIR 1 video, it is possible to provide a framework for x :
Visible spectrum images are more precise than IR spectrum images which tend to “bleed”.
So let's go back to our previous table with x=0,4 :
For the value of x=0,4 , the comparison matrix now reveals a singular relationship linking the volumes and surfaces of the parts :
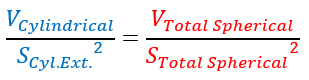
Which can also be written in the more elegant form :
For convenience, this relationship will be referred to as V/S² for the continuation of the study.
At this stage, it can only be asserted that the observed form actually presents a singular geometric relationship, which only appears for the observed height-to-length ratio, i.e. For x=0,4 (Verification available in Annex 3) :
The resolution of the relationship V/S² leads to a particular solution for x corresponding precisely to the value observed on the video. It is, therefore very unlikely that this particular solution will appear by chance.
This observation tends to demonstrate that the object is indeed the fruit of an ingenious design whose nature could be linked to the relationship V/S². If this is indeed the case, this relationship would, therefore also be the starting point for the design of the fuselage.
We will see subsequently that the relationship is, in reality the consequence of a more general relationship, which de facto excludes the possibility of a coincidence. However, talking about it here would make the reasoning anachronistic.
Could this be a lucky coincidence?
However weak it may be, the possibility of a coincidence must be considered but the noose tightens again when we study the aspect of compactness :
Compactness is defined by the ratio between the volume of an object and its surface area. It makes it possible to compare the ability of geometric shapes to encompass a maximum volume within a minimum surface area.
For illustration, the sphere is the most efficient shape with a compactness of :
Let us determine the compactness of the form TIC TAC :
Which, for x=2/5 , becomes :
We are now missing an estimate of R to give an approximate value of CTT.
Remember that the pilots estimated the length of the Tic-Tac at approximately 40 ft or approximately 12 m.
Let us also recall the definition of L on the diagram : L=l+2R
Which for x=2/5 becomes :
We can then give an estimate of the compactness of the Tic-Tac :
This result does not give us any certainty and only allows for speculations that are difficult to verify but which, nevertheless deserve to be presented.
The estimate of 40 ft length given by the pilot obviously contains an uncertainty, to which is added that of the conversion of ft into m. We can therefore reasonably ask whether the real compactness would not be 1.
If we consider that :
Then :
The length would then be :
Which would approximately correspond to 38 ft and prove to be compatible with the observation made by the pilots. On the basis of this hypothesis, we can therefore complete the initial diagram and risk giving an approximate prediction of the dimensions of the phenomenon :
It is, of course, surprising to note that two distinct reasonings can lead to concordant predictions, both with regard to the video (value of x=0,4) and the estimate of the length of the pilots (11.54 m versus 12.19 m). This concordance is, in itself, truly perplexing and tends a priori in favor of a judicious design.
For all practical purposes, the numerical values of the other geometric aspects are summarized below :
This concludes the first part.
The second part turns out to be more difficult to explain and much more mathematical but it is also the one which, in my opinion, is both the most convincing and the most astonishing.
What can we learn from the relationship V/S² ?
Let's recall the relationship :
In this form we cannot learn much more. We need to introduce a new aspect such as the expression of the volume and surface of the whole. The idea is simple and the result is very easy to demonstrate (demonstration available in annex 4) :
We therefore obtain this triple relationship which teaches us that from a geometric point of view the whole of the shape is also in relation to the different parts. Obviously, the constraints are even more specific than previously imagined.
It also shows the coefficient 25/13... which, to my knowledge, does not correspond to any constant in physics. Despite my research in the literature and engineering cheat sheets, I cannot find any correspondence for both the relationship and the coefficient 25/13.
The relationship does, however, allow one to "envision" a flow (possibly of an electromagnetic nature) exchanged between the different volumes through the different walls, but this is a purely speculative personal interpretation. The motivation for this relationship might as well be aesthetic after all.
If, like it does for me, the process seems interesting to you so far, this is where it really becomes confusing! I'll let you judge for yourself :
I will spare you the personal details that led me to this idea and take you directly to the results :
After countless attempts trying to find out more, I considered the possibility that the relationship was not unique to the TIC TAC. So I applied the relationship to other “geometrically neighboring” shapes. I'll let you judge the results :
(Details of the calculations for each form available in annex 5)
By applying the relation to different forms, we obtain different values for x but we still find the same coefficient 25/13 ! It therefore seems that what we initially considered to be a relationship specific to a single geometric shape is, in reality, a principle applicable to different shapes.
For convenience, I allowed myself to name it “Principle of Geometric Affinity” or PAG in reference to a 3rd unfinished part.
To this day, I am considering the possibility that this principle would make it possible to categorize shapes according to their symmetries. It would perhaps be possible to categorize the 25/13 family or other families yet to be discovered. The origin of this principle could also come from a consequence of LIE groups or even from the application of a Lagrangian to a still undetermined relation.
Whatever the case, the Principle of Geometric Affinity is a pure mathematical object and independent of the phenomenon, which puts us on its trail. This is a mathematical problem in its own right and must be addressed, explored and analyzed as such. The form of the TIC TAC would a priori only be an application of the Principle of Geometric Affinity. Being interested in the sole case of the TIC TAC can, therefore be likened to observing only one side of a die whose real size we still do not know.
It nonetheless, remains astonishing and even shocking that simple mathematical curiosity applied to a case of UAP could have led to such a discovery...
We wondered about the nature of the advantage that could have prevailed over aerodynamics. Given that this work has, so far not brought to light any constant of physics, and that the literature makes no mention of the relationship, we are not able to link our relationship to any physical or technical necessity. Despite significant progress, this aspect remains an enigma.
Annex 1 : Calculation
Annex 2 : Volumes and surfaces of each part and the whole
Annex 3 : Verifications on the V/S² relationship
For the value of x=0,4 and only for this value, the comparison table reveals a remarkable relationship specific to the geometry of Tic-Tac :
By returning to our first table (before the value of x=0,4 is not taken into account) we can establish the initial equation :
Note that this relationship is independent of R and depends only on x.
What are the solutions to this relationship? By expanding we obtain :
Then
which gives the quadratic equation :
So for the form
whose discriminant is written :
we deduce the roots :
We therefore find x=0,4 in perfect agreement with the observations of the FLIR1 video
Spherical solution (Corresponds to a solution where l=0)
The resolution of the relationship V/S² leads to a particular solution for x corresponding precisely to the value observed on the video. It is, therefore, very unlikely that this particular solution will appear by chance.
Annex 4 : Extension of the relationship V/S²
Let's calculate the ratios indicated in the first column before expressing them according to the surface area or the volume of the TIC TAC in the second column :
Using these new expressions and reminders, let's express the terms of the relationship V/S2 depending on STT And VTT :
By application of the relationship V/S², we obtain :
Let's check for what value(s) of x equality between the 3rd and 5th terms are valid by solving :
We find concordantly the value x=0,4 ; which supports our previous hypotheses and deductions. Now let's calculate the value of the terms :
It is thus demonstrated that for the particular value x=0,4 ; we can apply the relation :
Note that this formulation in no way presumes the value of R.
Annex 5 : Calculations applications of the principle of Geometric Affinity to different shapes
Let us recall the schematization of the phenomenon :
Let us recall the expression of l :
In the first part, we highlighted the particular value x :
The equality of the geometric affinity between the parts is, therefore, subject to the condition x=2/5.
Let us now compare the geometric affinity of the whole to those of each part :
We conclude that for the shape of the Tic-Tac, the geometric affinity relation is written :
SQUARE SECTION PRISM
As in the case of the Tic-Tac, only the surface facing the outside is taken into account.
For what x value can we observe the equality of geometric affinities between parts :
Let us compare the geometric affinity of the whole to those of each part :
In an absolutely astonishing way, we therefore find the geometric affinity relationship with the same factor 25/13 :
Would the ratio 25/13 correspond to a constant towards which the geometric affinities converge under certain conditions?
For all practical purposes, some interesting observations are added :
Let's calculate the compactness :
For x=4/13 :
It follows that if the compactness is 1 then R is worth 30/13 exactly as in the case of the Tic-Tac…
It is very surprising to find so many common results between two very different forms.
Note also that :
CYLINDER
The shape is reminiscent of certain cases of “cigar” shaped UAP.
Schematize the form like this :
As in the case of the Tic-Tac, only the surface facing the outside is taken into account.
For what x value can we observe the equality of the geometric affinities of the parts :
Let us compare the geometric affinity of the whole to those of each part :
Just as astonishingly, we once again find the geometric affinity relationship with the same factor 25/13 :
For all practical purposes, some interesting observations are added :
Let's calculate the compactness :
Since here too x=4/13 :
Likewise if C=1 so R=30/13 once again exactly as in the case of Tic-Tac.
Amazingly, it turns out that the compactness of the cylinder is exactly the same as that of the previous square section paving stone.
PRISM WITH HEXAGONAL SECTION
Schematize the form like this :
As in the previous cases, only the surface facing the outside is taken into account.
Under these conditions, the internal radius of the hexagon is worth :
For what x value can we observe the equality of the geometric affinities of the parts :
Let us compare the geometric affinity of the whole to those of each part :
Still with the same astonishment, we once again find the geometric affinity relationship with the same factor 25/13 :
Only the last term seems to suggest a variation depending on the geometric shape. It is very surprising to note the success of the geometric affinity relation in these few tests.
For all practical purposes, some interesting observations are added :
Let's calculate the compactness :
Since here too x=4/13 :
Likewise if C=1 so R=30/13 once again exactly as in the case of Tic-Tac.
Amazingly, it turns out that the compactness of the hexagonal prism is exactly the same as that of the square block and the triple cylinder.